# 时间复杂度
- 常数时间的操作,一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
- 时间复杂度为一个算法流程中,常数操作数量的一个指标,O (读作 big O) 来表示,具体来说先要对一个算法流程非常熟悉,然后去写出这个算法流程中发生了多少常数操作,进而总结出常数操作数量的表达式。
- 在表达式中,只要高阶项,不要低阶项,也不要高阶项系数,剩下的部分如果为 f (N), 那么时间复杂度为 O (f (N))。
- 评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是常数项时间。
# 大 O 表示法
大 O 符号,又叫做道朗符号,是数学中用另一个较为简单的函数去描述函数渐进行为的一个符号,用来刻画被截断的无穷级数尤其是渐近级数的剩余项。
# 常见复杂度量级
| 分类 | 记作 |
|---|---|
| 常量阶 | O(1) |
| 对数阶 | O(logn) |
| 线性阶 | O(n) |
| 线性对数阶 | O(nlogn) |
| n 方阶 | O(nⁿ) |
| 指数阶 | O(2ⁿ) |
| 阶乘阶 | O(n!) |
# 常见时间复杂度
- O(1)->HashMap
- O (logn)-> 二叉树
- O (N)->for 循环
- O (nlogn)->for 循环嵌套二叉树
- O (n2)->for 循环嵌套 for 循环
# 时间复杂度大小依次
O(1)<O(log₂n)<O(n)<O(nlog₂n)<O(n²)<O(n³)<O(2¹)<O(n!)
# 时间复杂度如何计算
常量阶:只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度都记作 O (1)
。或者说,一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是 Ο(1)。对数阶:
i=1;
while(i<=n){
i=i*2;
}分析上段代码,i 的取值是一个首项为 1,公差为 2 的等比数列: 2º・2¹・2²・2³・・・・2ⁿⁿ = n,其中 nn 即为项数,求对数即
nn=log₂n。时间复杂度为 O (log₂n)。线性阶、n 方阶:一般情况下,如果循环体内循环控制变量为线性增长,那么包含该循环的算法的时间复杂度为 O (n)
,线性阶嵌套线性阶的算法时间复杂度为 O (nⁿ),涉及下文乘法法则。线性对数阶:当一个线性阶代码段法嵌套一个对数阶代码段,该算法的时间复杂度为 O (nlogn)
指数阶和阶乘阶:根据函数,随着 n 的增加,运行时间会无限急剧增加,因此效率非常低下。
# 3 个分析时间复杂度的方法
最大阶法则:忽略式子中的常量,低阶,系数,只计算最大阶的量级。
说白了就只关注循环次数最多的代码段。int fun(int n) {
int sum1 = 0;
int i = 1;
int j = 1;
for (; i <= n; ++i) {
sum = sum + i;
}for (; i <= n; ++i) {
for (; i <= n; ++i) {
sum + = i+j;
}}return sum;
}加法法则:总复杂度等于量级最大代码段的复杂度,公式:
T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))
int fun(int n) {
int sum_1 = 0;
int p = 1;
for (; p < 100; ++p) {
sum_1 = sum_1 + p;
}int sum_2 = 0;
int q = 1;
for (; q < n; ++q) {
sum_2 = sum_2 + q;
}int sum_3 = 0;
int i = 1;
int j = 1;
for (; i <= n; ++i) {
j = 1;
for (; j <= n; ++j) {
sum_3 = sum_3 + i * j;
}}return sum_1 + sum_2 + sum_3;
}三段代码的复杂度分别是 O (1)、O (n)、O (n²),根据法则:T (n)=T1 (n)+T2 (n)=max (O (f (n)), O (g (n))) =O (max (f (n), g (n)))。即为 O (n²)。
乘法法则:嵌套代码复杂度等于嵌套内外代码复杂度之积。公式:
T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))
int fun1(int n) {
int ret = 0;
int i = 1;**加粗样式**
for (; i < n; ++i) {
ret = ret + fun2(i);
}}int fun2(int n) {
int sum = 0;
int i = 1;
for (; i < n; ++i) {
sum = sum + i;
}return sum;
}fun1 方法中,忽略掉 fun2 () 的调用复杂度为 O (n)。fun2 方法的时间复杂度是 O (n),根据法则,T (n) = T1 (n) * T2 (n) = O (n*n) = O (n²)。
其中比较特殊的一种不符合上述 3 个法则:
int fun(int m, int n) {
int sum_1 = 0;
int i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}int sum_2 = 0;
int j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}return sum_1 + sum_2;
}当前复杂度有两种数据规模 m 和 n 确定,加法法则应更正为:T1 (m) + T2 (n) = O (f (m) + g (n)),即时间复杂度为 O (m+n)。
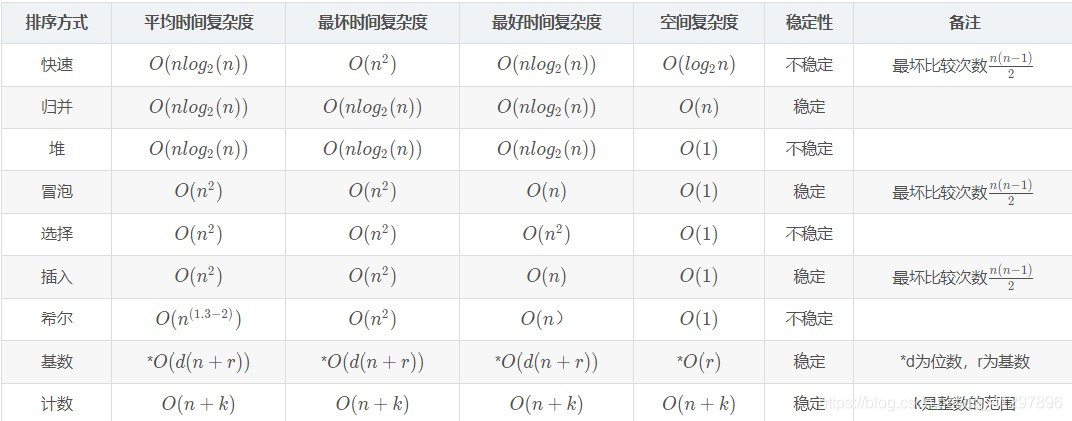
常用大 O 来表述,这个函数描述了算法执行所要时间的增长速度,记作 f (n)。算法需要执行的运算次数(用函数表示)记作 T (n)。存在常数 c
和函数 f (n),使得当 n >= c 时 T (n) <= f (n),记作 T (n) = O (f (n)),其中,n 代表数据规模也就是输入的数据。常见排序复杂度如图:![img_1.png]()
# 选择排序
import java.util.Arrays; | |
/** | |
* @Author: LightRain | |
* @Description: 选择排序算法 | |
* @DateTime: 2023-04-27 17:15 | |
* @Version:1.0 | |
**/ | |
public class SelectSort { | |
public static void main(String[] args) { | |
int[] arr = new int[]{90, 61, 92, 31, 78, 59}; | |
selectionSort(arr); | |
System.out.println("Arrays.stream(arr).toArray() = " + Arrays.toString(Arrays.stream(arr).toArray())); | |
} | |
private static void selectionSort(int[] arr) { | |
if (arr == null || arr.length < 2) { | |
return; | |
} | |
//i~N-1 | |
for (int i = 0; i < arr.length - 1; i++) { | |
int minIndex = i; | |
//i~N-1 上找到最小值的下标 | |
for (int j = i + 1; j < arr.length; j++) { | |
minIndex = arr[j] < arr[minIndex] ? j : minIndex; | |
} | |
swap(arr, i, minIndex); | |
} | |
} | |
private static void swap(int[] arr, int i, int j) { | |
int tmp = arr[i]; | |
arr[i] = arr[j]; | |
arr[j] = tmp; | |
} | |
} |
# 冒泡排序
import java.util.Arrays; | |
/** | |
* @Author: LightRain | |
* @Description: 冒泡排序 | |
* @DateTime: 2023-04-27 19:12 | |
* @Version:1.0 | |
**/ | |
public class BubbleSort { | |
public static void main(String[] args) { | |
int[] arr = new int[]{90, 62, 92, 31, 78, 59}; | |
bubbleSort(arr); | |
System.out.println("Arrays.stream(arr).toArray() = " + Arrays.toString(Arrays.stream(arr).toArray())); | |
} | |
private static void bubbleSort(int[] arr) { | |
if (arr == null || arr.length < 2) { | |
return; | |
} | |
//0~end | |
for (int end = arr.length - 1; end > 0; end--) { | |
for (int i = 0; i < end; i++) { | |
if (arr[i] > arr[i + 1]) { | |
swap(arr, i, i + 1); | |
} | |
} | |
} | |
} | |
private static void swap(int[] arr, int i, int j) { | |
// 不推荐使用 | |
// arr[i] = arr[i] ^ arr[j]; | |
// arr[j] = arr[i] ^ arr[j]; | |
// arr[i] = arr[i] ^ arr[j]; | |
int tmp = arr[i]; | |
arr[i] = arr[j]; | |
arr[j] = tmp; | |
} | |
} |
# 插入排序
import java.util.Arrays; | |
/** | |
* @Author: LightRain | |
* @Description: 插入排序 | |
* @DateTime: 2023-04-27 19:32 | |
* @Version:1.0 | |
**/ | |
public class InsertSort { | |
public static void main(String[] args) { | |
int[] arr = new int[]{90, 62, 92, 31, 78, 59}; | |
insertSort(arr); | |
System.out.println("Arrays.stream(arr).toArray() = " + Arrays.toString(Arrays.stream(arr).toArray())); | |
} | |
private static void insertSort(int[] arr) { | |
if (arr == null || arr.length < 2) { | |
return; | |
} | |
//0~i 想有序 | |
for (int i = 1; i < arr.length; i++) { | |
// 做到 0~i 有序 | |
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) { | |
swap(arr, j, j + 1); | |
} | |
} | |
} | |
private static void swap(int[] arr, int i, int j) { | |
int tmp = arr[i]; | |
arr[i] = arr[j]; | |
arr[j] = tmp; | |
} | |
} |
# 查找出数组中奇数元素
/** | |
* @Author: LightRain | |
* @Description: 查找出数组中的奇数元素 | |
* @DateTime: 2023-04-27 22:08 | |
* @Version:1.0 | |
**/ | |
public class EvenTimesOddTimes { | |
public static void main(String[] args) { | |
int[] arr = new int[]{1, 1, 2, 2, 3}; | |
printOddTimesNum1(arr); | |
} | |
private static void printOddTimesNum1(int[] arr) { | |
int eor = 0; | |
for (int cur : arr) { | |
eor ^= cur; | |
} | |
System.out.println("eor = " + eor); | |
} | |
} |
# 查找出数组中的两个奇数元素
/** | |
* @Author: LightRain | |
* @Description: 查找出数组中的两个奇数元素 | |
* @DateTime: 2023-04-27 22:37 | |
* @Version:1.0 | |
**/ | |
public class EvenTimesOddTimes { | |
public static void main(String[] args) { | |
int[] arr = new int[]{1, 1, 2, 2, 3, 4}; | |
printOddTimesNum2(arr); | |
} | |
private static void printOddTimesNum2(int[] arr) { | |
int eor = 0; | |
for (int cur : arr) { | |
eor ^= cur; | |
} | |
// 提取出最右的 1 | |
int rightOne = eor & (~eor + 1); | |
int onlyOne = 0; | |
for (int cur : arr) { | |
if ((cur & rightOne) == rightOne) { | |
onlyOne ^= cur; | |
} | |
} | |
System.out.println(onlyOne + " " + (eor ^ onlyOne)); | |
} | |
} |
# 二分法的详解与扩展
- 在一个有序数组中,找某个数是否存在
- 在一个有序数组中,找 >= 某个数最左侧的位置
- 局部最小问题
# 对数器
import java.util.Arrays; | |
/** | |
* 以排序算法为例: | |
* 实现对数器的核心步骤: | |
* 1. 实现生成随机数组的方法 | |
* 2. 实现判断两个数组是否完全相等的方法 | |
* 3. 实现一个完全正确的方法 b | |
* 4. 实现需要测试的方法 a | |
*/ | |
public class LogarithmicDevice { | |
public static void main(String[] args) { | |
// 测试次数,也就是测试案例的个数 50 万个 | |
int testTime = 500000; | |
// 随机数组最大容量 | |
int maxSize = 100; | |
// 随即数组元素最大值 | |
int maxValue = 100; | |
// 方法 a 成功的标志,默认方法 a 可行 | |
boolean succeed = true; | |
// 循环测试 500000 次,但凡有一次方法 a 行不通就退出 | |
for (int i = 0; i < testTime; i++) { | |
// 获取一个随机数组,拿给方法 a 执行 | |
int[] arr1 = generateRandomArray(maxSize, maxValue); | |
// 将这个随机数组拷贝一份,拿给方法 b 执行 | |
int[] arr2 = Arrays.copyOf(arr1, arr1.length); | |
//1. 使用方法 a 对数组进行排序 | |
selectSort(arr1); | |
//2. 使用方法 b 对数组进行排序 | |
comparator(arr2); | |
//3. 判断排序过后的 arr1 与 arr2 是否完全一样 | |
if (!isEqual(arr1, arr2)) { | |
// 进入到这里说明某一次比较中,arr1 与 arr2 排序后不一样 | |
// 将标记置为 false | |
succeed = false; | |
// 使用数组工具类将 arr1 打印出来,以便于后续的手动查看错误 | |
Arrays.toString(arr1); | |
// 使用数组工具类将 arr2 打印出来,以便于后续的手动查看错误 | |
Arrays.toString(arr2); | |
break;// 退出循环比较过程,因为已经没必要继续比较了 | |
} | |
} | |
// 通过三目运算符输出方法 a 是否可行 | |
System.out.println(succeed ? "方法a可行!" : "方法a有错误!"); | |
} | |
/** | |
* 1. 实现生成随机数组的方法(数组大小随机,数组元素个数随机) | |
* | |
* @param maxSize 生成的随机数组的最大容量 | |
* @param maxValue 生成的随机数组的元素最大值 | |
* @return 返回生成好的随机数组 | |
*/ | |
public static int[] generateRandomArray(int maxSize, int maxValue) { | |
//1. 初始化数组的容量,使用随机数的方式 | |
//Math.random () 函数生成一个 double 类型的小数,值在 [0,1) 之间 | |
int[] arr = new int[(int) (Math.random() * (maxSize + 1))]; | |
//2. 给数组赋值,以随机数的方式 | |
// 解释为什么要减去一个随机数: | |
// 因为两个随机数不一样,相减是为了产生负数,使我的数组元素正负都有 | |
for (int i = 0; i < arr.length; i++) { | |
arr[i] = (int) (Math.random() * (maxValue + 1)) - (int) (Math.random() * maxValue); | |
} | |
//3. 将随机生成的数组返回 | |
return arr; | |
} | |
/** | |
* 2. 实现一个比较器(其实就是我的方法 b,是一个确保了正确率的方法) | |
* | |
* @arr 待排序的数组 | |
*/ | |
public static void comparator(int[] arr) { | |
// 使用数组工具类自带的排序方法,保证是正确的 | |
Arrays.sort(arr); | |
} | |
/** | |
* 3. 实现一个方法,判断数组 arr1 和数组 arr2 是否完全相等 | |
* | |
* @param arr1 数组 1 | |
* @param arr2 数组 2 | |
* @return 完全相等返回 true,但凡有一点不同就返回 false | |
*/ | |
public static boolean isEqual(int[] arr1, int[] arr2) { | |
//1. 一个数组为 null,一个数组不为 null,直接返回 false | |
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) { | |
return false; | |
} | |
//2.arr1 与 arr2 数组同为空 | |
if (arr1 == null && arr2 == null) { | |
return true; | |
} | |
//3.arr1 与 arr2 长度不相等,直接返回 false | |
if (arr1.length != arr2.length) { | |
return false; | |
} | |
//4. 此时 arr1 与 arr2 都不为空且长度相同,循环遍历依次比较,一个元素不一样直接返回 false | |
for (int i = 0; i < arr1.length; i++) { | |
if (arr1[i] != arr2[i]) | |
return false; | |
} | |
//5. 程序执行到这里说明 arr1 与 arr2 完全相同,直接返回 true | |
return true; | |
} | |
/** | |
* 4. 需要测试的方法 a,这里以选择排序为例 | |
* | |
* @param arr 待排序的数组 | |
*/ | |
public static void selectSort(int[] arr) { | |
// 数组为 null,或者数组长度小于 2,直接返回 | |
if (arr == null || arr.length < 2) { | |
return; | |
} | |
// 外层 for,控制每一趟在 i ~ n - 1 范围查找最小值 | |
for (int i = 0; i < arr.length; i++) { | |
// 最小值下标,默认为每一趟的起始位置 i | |
int minIndex = i; | |
// 内存 for,在具体的 i~n -1 范围内查找最小值 1 | |
for (int j = i; j < arr.length; j++) { | |
minIndex = arr[minIndex] > arr[j] ? j : minIndex; | |
} | |
// 交换每一趟起始位置 i 与该范围最小值所在的位置 | |
int temp = arr[minIndex]; | |
arr[minIndex] = arr[i]; | |
arr[i] = temp; | |
} | |
} | |
} |