# Specification

This document is the community review draft of the JSR-133 specification, the Java Memory Model (JMM) and Thread Specification. This specification is intended to be part of the JSR-176 umbrella for the Tiger (1.5) release of Java, and is intended to replace Chapter 17 of the Java Language Specification and Chapter 8 of the Java Virtual Machine Specification. The current draft has been written generically to apply to both, the final version will include two different versions, essentially identical in semantics but using the appropriate terminology for each.
The discussion and development of this specification has been unusally detailed and tech-nical, involving insights and advances in a number of academic topics.
This discussion is archived (and continues) at the JMM web site http://www.cs.umd.edu/~pugh/java/memoryModel.
The web site provides additional information that may help in understanding how this spec-ification was arrived at.
The core semantics (Sections 4 – 7) is intended to describe semantics allowed by existing JVMs.
The existing chapters of the JLS and JVMS specify semantics that are at odds with optimizations performed by many existing JVMs. The proposed core semantics should not cause issues for existing JVM implementations, although they may limit potential future optimizations and implementations.
The expert group seeks feedback on two technical issues: a choice of a weak or strong causality model (Section 7.4), and an issue regarding the semantics of notify and interrupt(Section 12.4).
The JSR-133 expert group urges all readers to examine these issues and provide the expert group with feedback on them.
The weak causality model could allow more compiler optimizations, the strong model could provide more safety guarantees. However, we have not found any compelling and realistic examples of optimizations or guarantees that would guide the choice between the strong and weak causality model. This document proposes the strong causality model, since any JVM that is compliant with the strong causality model will also be compliant with the weak causality model.
JCP members are also urged to closely read the semantics on final fields (Sections 3.5 and 8). This is the one place most likely to require JVM implementors to change their implementation to be compliant with JSR-133. In particular, memory barriers or other techniques may be required to ensure that other threads see the correct values for final fields of immutable objects, even in the presence of data races.

# Introduction

Java virtual machines support multiple threads of execution. Threads are represented in Java by the Thread class. The only way for a user to create a thread is to create an object of this class; each Java thread is associated with such an object. A thread will start when the start() method is invoked on the corresponding Thread object.
The behavior of threads, particularly when not correctly synchronized, can be particularly confusing and intuitive. This specification describes the semantics of multithreaded Java programs, including rules on what values may be seen by a read of shared memory that is updated by other threads. Similar to the memory model for different hardware architectures, these semantics have been referred to as the Java memory mode.
These semantics do not describe how a multithreaded program should be executed.
Rather, they describe only the behaviors that are allowed by multithreaded programs. Any execution strategy that generates only allowed behaviors is an acceptable execution strategy. This is discussed more in Appendix A.

# Locks

Java provides multiple mechanisms for communicating between threads. The most basic of these methods is synchronization, which is implemented using monitors. Each object in Java is associated with a monitor, which a thread can lock or unlock. Only one thread at a time may hold a lock on a monitor. Any other threads attempting to lock that monitor are blocked until they can obtain a lock on that monitor.
A thread t may lock a particular monitor multiple times; each unlock reverses the effect of one lock operation.
The Java programming language does not provide a way to perform separate lock and unlock actions; instead, they are implicitly performed by high-level constructs that always arrange to pair such actions correctly.
Note, however, that the Java virtual machine provides separate monitorenter and moni-torexit instructions that implement the lock and unlock actions.
The synchronized statement computes a reference to an object; it then attempts to perform a lock action on that object’s monitor and does not proceed further until the lock action has successfully completed. After the lock action has been performed, the body of the synchronized statement is executed. If execution of the body is ever completed, either normally or abruptly, an unlock action is automatically performed on that same monitor.
A synchronized method automatically performs a lock action when it is invoked; its body is not executed until the lock action has successfully completed. If the method is an instance method, it locks the monitor associated with the instance for which it was invoked (that is, the object that will be known as this during execution of the body of the method).
If the method is static, it locks the monitor associated with the Class object that represents the class in which the method is defined. If execution of the method’s body is ever completed, either normally or abruptly, an unlock action is automatically performed on that same monitor.

The Java programming language does not prevent, nor require detection of, deadlock con-ditions. Programs where threads hold (directly or indirectly) locks on multiple objects should use conventional techniques for deadlock avoidance, creating higher-level locking primitives that don’t deadlock, if necessary.
There is a total order over all lock and unlock actions performed by an execution of a program.

# Notation in examples

The Java memory model is not substantially intertwined with the Object-Oriented nature of the Java programming language. For terseness and simplicity in our examples, we often exhibit code fragments that could as easily be C or Pascal code fragments, without class or method definitions, or explicit dereferencing. Instead, most examples consists of two or more threads containing statements with access to local variables (e.g., local variables of a method, not accessible to other threads), shared global variables (which might be static fields) or instance fields of an object.

# Incorrectly synchronized programs can exhibit sur-prising behaviors

The semantics of the Java programming language allow compilers and microprocessors to perform optimizations that can interact with incorrectly synchronized code in ways that can produce behaviors that seem paradoxical.
Consider, for example, Figure 1. This program contains local variables r1 and r2; it also contains shared variables A and B, which are fields of an object. It may appear that the result r2 == 2, r1 == 1 is impossible. Intuitively, if r2 is 2, then instruction 4 came before instruction 1. Further, if r1 is 1, then instruction 2 came before instruction 3. So, if r2 == 2 and r1 == 1, then instruction 4 came before instruction 1, which comes before instruction 2, which came before instruction 3, which comes before instruction 4. This is, on the face of it, absurd.
However, compilers are allowed to reorder the instructions in each thread. If instruction 3 is made to execute after instruction 4, and instruction 1 is made to execute after instruction 2, then the result r2 == 2 and r1 == 1 is perfectly reasonable.

To some programmers, this behavior may make it seem as if their code is being “broken” by Java. However, it should be noted that this code is improperly synchronized:

• there is a write in one thread,
• a read of the same variable by another thread,
• and the write and read are not ordered by synchronization.

This is called a data race. When code contains a data race, counter-intuitive results are often possible.
Several mechanisms can affect this reordering: the just-in-time compiler and the processor may rearrange code. In addition, the memory hierarchy of the architecture on which a virtual machine is run may make it appear as if code is being reordered. For the purposes of simplicity, we shall simply refer to anything that can reorder code as being a compiler. Source code to bytecode transformation, which is traditionally thought of as compilation, is outside the scope of this document.
Another example of surprising results can be seen in Figure 2. This program is incorrectly synchronized; it accesses shared memory without enforcing any ordering between those ac-cesses. One common compiler optimization involves having the value read for m reused for o: they are both reads of p.x with no intervening write.
Now consider the case where the assignment to p.x in Thread 2 happens between the first read of p.x and the read of q.x in Thread 1. If the compiler decides to reuse the value of p.x for the second read, then m and o will have the value 0, and n will have the value 3. This may seem counter-intuitive as well: from the perspective of the programmer, the value stored at p.x has changed from 0 to 3 and then changed back.
Although this behavior is surprising, it is allowed by most JVMs. However, it is forbidden by the original Java memory model in the JLS and JVMS, one of the first indications that the original JMM needed to be replaced.

# Informal Semantics

A program must be correctly synchronized to avoid the kinds of non-intuitive behaviors that can be observed when code is reordered. The use of correct synchronization does not ensure that the overall behavior of a program is correct. However, its use does allow a programmer to reason about the possible behaviors of a program in a simple way; the behavior of a correctly synchronized program is much less dependent on possible reorderings. Without correct synchronization, very strange, confusing and counter-intuitive behaviors are possible.
There are two key ideas to understanding whether a program is correctly synchronized:
Conflicting Accesses Two accesses (reads of or writes to) the same shared field or array element are said to be conflicting if at least one of the accesses is a write.
Happens-Before Relationship Two actions can be ordered by a happens-before relation-ship. If one action happens before another, then the first is visible to and ordered before the second. There are a number of ways to induce a happens-before ordering in a Java program, including:

• Each action in a thread happens before every subsequent action in that thread.
• An unlock on a monitor happens before every subsequent lock on that monitor.
• A write to a volatile field happens before every subsequent read of that volatile.
• A call to start() on a thread happens before any actions in the started thread.
• All actions in a thread happen before any other thread successfully returns from a join() on that thread.
• If an action a happens before an action b, and b happens before an action c, then a happens before c.

When a program contains two conflicting accesses that are not ordered by a happens-before relationship, it is said to contain a data race. A correctly synchronized program is one that has no data races (Section 3.4 contains a subtle but important clarification).
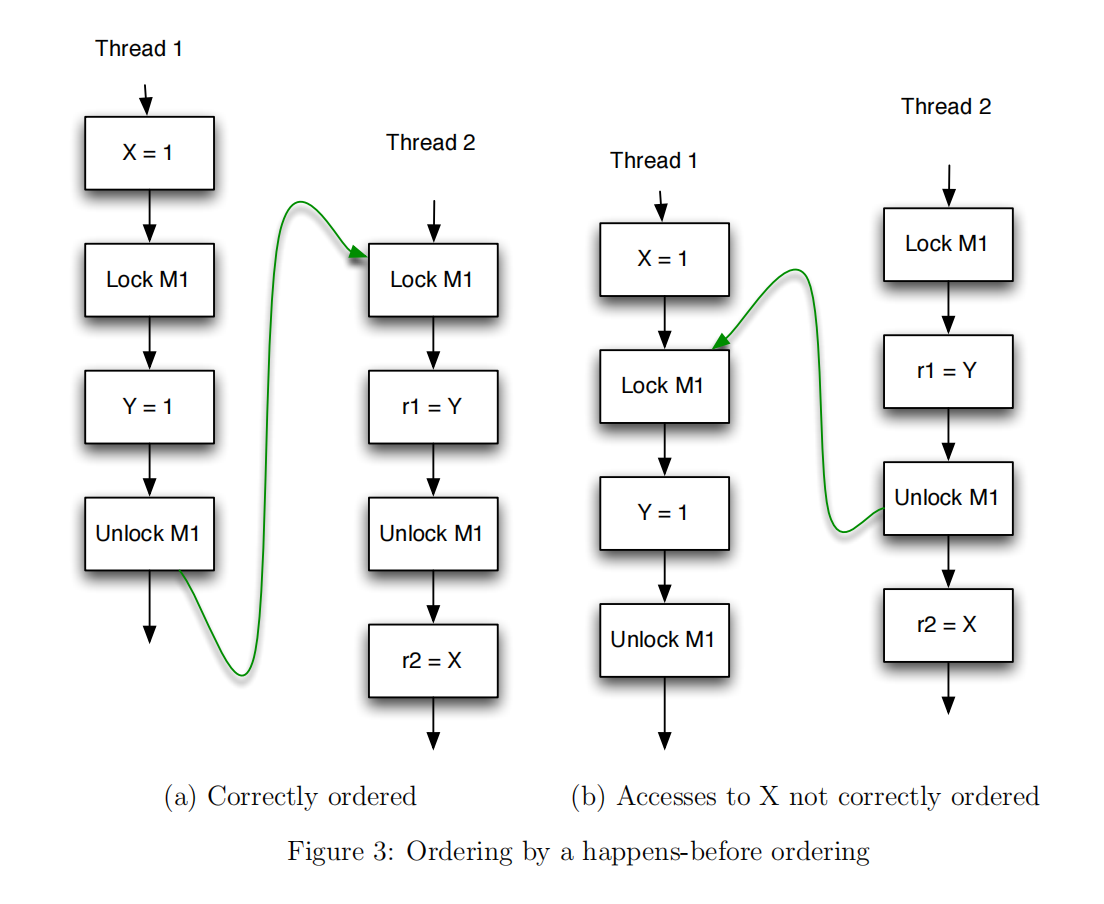
An example of incorrectly synchronized code can be seen in Figure 3, which shows two different executions of the same program, both of which contain conflicting accesses to shared variables X and Y. In Figure 3a, the two threads lock and unlock a monitor M1 so that, in this execution, there is a happens-before relationship between all pairs of conflicting accesses. However, a different execution, shown in Figure 3b, shows why this program is incorrectly synchronized; there is no happens-before ordering between the conflicting accesses to X.
If a program is not correctly synchronized, then three types of problems can appear:visibility, ordering and atomicity.

class LoopMayNeverEnd {

    boolean done = false;

    void work() {

        while (!done) {

            // do work

        }

    }

    void stopWork() {

        done = true;

    }

}

//                       Figure 4: Visibility Example

# Visibility

If an action in one thread is visible to another thread, then the result of that action can be observed by the second thread. The results of one action are only guaranteed to be visible to a second action if the first happens before the second.
Consider the code in Figure 4. Now imagine that two threads are created, and that one thread calls work(), and at some point, the other thread calls stopWork(). Because there is no happens-before relationship between the two threads, the thread in the loop may never see the update to done performed by the other thread. In practice, this may happen if the compiler detects that there are no updates to done in the first thread: the loop can be transformed to an infinite loop.
To ensure that this does not happen, there must be a happens-before relationship be-tween the two threads. In LoopMayNeverEnd, this can be achieved by declaring done to be volatile. All actions on volatiles happen in a total order, and each write to a volatile field happens before any subsequent read of that volatile.

# Ordering

Ordering constraints govern the order in which multiple actions are seen to have happened.
The ability to perceive ordering constraints among actions is only guaranteed to actions that share a happens-before relationship with them.
The code in Figure 5 shows an example of where the lack of ordering constraints can produce surprising results. Consider what happens if sideOne() gets executed in one thread and sideTwo() gets executed in another. Would it be possible for temp1 and temp2 both to be true?

class BadlyOrdered {

    boolean a = false;

    boolean b = false;

    boolean sideOne() {

        boolean temp1 = b; // 1

        a = true; // 2

        return temp1;

    }

    boolean sideTwo() {

        boolean temp2 = a; // 3

        b = true; // 4

        return temp2;

    }

}

//                       Figure 5: Ordering example

The Java memory model allows this result, illustrating a violation of the ordering that a user might have expected. This code fragment is not correctly synchronized (the conflicting accesses are not ordered by a happens-before ordering).
If ordering is not guaranteed, then the actions labeled 2 and 4 can appear to happen before the actions labeled 1 and 3; both reads can then see the value true. Compilers have substantial freedom to reorder code in the absence of synchronization, so a compiler could move the assignments to a and b earlier, resulting in temp1 and temp2 both being true.

# Atomicity

If an action is (or a set of actions are) atomic, its result must be seen to happen “all at once”, or indivisibly. Section 10 discusses some atomicity issues for Java; other than the exceptions mentioned there, all individual read and write actions take place atomically.
Atomicity can also be enforced between multiple actions. A program can be free from data races without having this form of atomicity. However, it is frequently just as important to enforce appropriate atomicity in a program as it is to enforce freedom from data races. Consider the code in Figure 6. Since all access to the shared variable balance is guarded by synchronization, the code is free of data races.
Now assume that one thread calls deposit(5), while another calls withdraw(5); there is an initial balance of 10. Ideally, at the end of these two calls, there would still be a balance of 10. However, consider what would happen if:

• The deposit() method sees a value of 10 for the balance, then

class BrokenBankAccount {

    private int balance;

    synchronized int getBalance() {

        return balance;

    }

    synchronized void setBalance(int x) throws IllegalStateException {

        balance = x;

        if (balance < 0) {

            throw new IllegalStateException("Negative Balance");

        }

    }

    void deposit(int x) {

        int b = getBalance();

        setBalance(b + x);

    }

    void withdraw(int x) {

        int b = getBalance();

        setBalance(b - x);

    }

}

//                       Figure 6:Atomicity Example

• The withdraw() method sees a value of 10 for the balance and withdraws 5, leaving a balance of 5, and finally
• The deposit() method uses the balance it originally saw to calculate the new balance.

As a result of this lack of atomicity, the balance is 15 instead of 10. This effect is often referred to as a lost update because the withdrawal is lost. A programmer writing multi-threaded code must use synchronization carefully to avoid this sort of error. For this example, making the deposit() and withdraw() methods synchronized will ensure that the actions of those methods take place atomically.

# Sequential Consistency

If a program has no data races, then executions of the program are sequentially consistent:very strong guarantees are made about visibility and ordering. Within a sequentially con-sistent execution, there is a total order over all individual actions (such as a read or a write)which is consistent with program order. Each individual action is atomic and is immedi-ately visible to every thread. As noted before, sequential consistency and/or freedom from data races still allows errors arising from groups of operations that need to be perceived atomically, as shown in Figure 6.
Having defined sequential consistency, we can use it to provide an important clarification regarding correctly synchronized programs. A program is correctly synchronized if and only if all sequentially consistent executions are free of data races. Programmers therefore only need to reason about sequentially consistent executions to determine if their programs are correctly synchronized.
A more full and formal treatment of memory model issues for normal fields is given in Sections 4–7.

# Final Fields

Fields declared final can be initialized once, but never changed. The detailed semantics of final fields are somewhat different from those of normal fields. In particular, compilers have a great deal of freedom to move reads of final fields across synchronization barriers and calls to arbitrary or unknown methods. Correspondingly, compilers are allowed to keep the value of a final field cached in a register and not reload it from memory in situations where a non-final field would have to be reloaded.
Final fields also allow programmers to implement thread-safe immutable objects without synchronization. A thread-safe immutable object is seen as immutable by all threads, even if a data race is used to pass references to the immutable object between threads. This can provide safety guarantees against misuse of the immutable class by incorrect or malicious code.
Final fields must be used correctly to provide a guarantee of immutability. An object is considered to be completely initialized when its constructor finishes. A thread that can only

class FinalFieldExample {

    final int x;

    int y;

    static FinalFieldExample f;

    public FinalFieldExample() {

        x = 3;

        y = 4;

    }

    static void writer() {

        f = new FinalFieldExample();

    }

    static void reader() {

        if (f != null) {

            int i = f.x;

            int j = f.y;

        }

    }

}

//                       Figure 7:Example illustrating final fields semantics

see a reference to an object after that object has been completely initialized is guaranteed to see the correctly initialized values for that object’s final fields.
The usage model for final fields is a simple one. Set the final fields for an object in that object’s constructor. Do not write a reference to the object being constructed in a place where another thread can see it before the object is completely initialized. When the object is seen by another thread, that thread will always see the correctly constructed version of that object’s final fields, and any object or array referenced by those final fields.
Figure 7 gives an example that demonstrates how final fields compare to normal fields. The class FinalFieldExample has a final int field x and a non-final int field y. One thread might execute the method writer(), and another might execute the method reader(). Because writer() writes f after the object’s constructor finishes, the reader() will be guaranteed to see the properly initialized value for f.x: it will read the value 3. However, f.y is not final; the reader() method is therefore not guaranteed to see the value 4 for it. Final fields are designed to allow for necessary security guarantees.
Consider the code in Figure 8. String objects are intended to be immutable and string operations do not perform synchronization. While the String implementation does not have any data races, other code could have data races involving the use of Strings, and the JLS

makes weak guarantees for programs that have data races. In particular, if the fields of the String class were not final, then it would be possible (although unlikely in the extreme) that thread 2 could initially see the default value of 0 for the offset of the string object, allowing it to compare as equal to "/tmp". A later operation on the String object might see the correct offset of 4, so that the String object is perceived as being "/usr". Many security features of the Java programming language depend upon Strings being perceived as truly immutable.
This is only an overview of the semantics of final fields. For a more detailed discussion, which includes several cases not mentioned here, consult Section 8.

# The Java Memory Model

A memory model describes, given a program and an execution trace of that program, whether the execution trace is a legal execution of the program. Java’s memory model works by examining each read in an execution trace and checking that the write observed by that read is valid.
A high level, informal overview of the memory model shows it to be a set of rules for when writes by one thread are visible to another thread. Informally, a read r can see the value of any write w such that w does not occur after r and w is not seen to be overwritten by another write w 0 (from r’s perspective).
When we use the term “read” in this memory model, we are only referring to values returned from fields or array elements. There are other actions performed by a virtual ma-chine, including reads of array lengths, executions of checked casts, and invocations of virtual methods, that must always return the correct value. Although these may be implemented with reads at the machine level, these actions cannot throw an exception or otherwise cause the VM to misbehave (e.g., crash or report the wrong array length).
The memory semantics determine what values can be read at every point in the program. The actions of each thread in isolation must behave as governed by the semantics of that thread, with the exception that the values seen by each read are determined by the memory model. We refer to this as obeying intra-thread semantics.
However, when threads interact, reads can return values written by writes from different threads. The model provides two main guarantees for the values seen by reads.

• Consistency requires that behavior is consistent with both intra-thread semantics and the write visibility enforced by the happens-before ordering.
• Causality means that an action cannot cause itself to happen. In other words, it must be possible to explain how the actions occurred in an execution without depending on one of the actions that you are trying to explain.
  Causality is necessary to ensure that correctly synchronized programs have sequentially consistent semantics. This is covered in more detail in Section 6.

# Definitions

Shared variables/Heap memory Memory that can be shared between threads is called shared or heap memory. All instance fields, static fields and array elements are stored in heap memory. We use the term variable to refer to both fields and array elements. Variables local to a method are never shared between threads.

Inter-thread Actions An inter-thread action is an action performed by a thread that could be detected by or be directly influenced by another thread. Inter-thread actions include reads and writes of shared variables and synchronization actions, such as obtaining or releasing a lock, reading or writing a shared variable, or starting a thread.
We do not need to concern ourselves with intra-thread actions (e.g., adding two local variables and storing the result in a third local variable).
An inter-thread action is annotated with information about the execution of that action. All actions are annotated with the thread in which they occur and the program order in which they occur within that thread. Some additional annotations include:

• write The variable written to and the value written.
• read The variable read and the write seen (from this, we can determine the value seen).
• lock The monitor which is locked.
• unlock The monitor which is unlocked.

For brevity’s sake, we usually refer to inter-thread actions as simply actions.

Program Order Among all the inter-thread actions performed by each thread t, the program order of t is a total order that reflects the order in which these actions would be performed according to the intra-thread semantics of t.

Intra-thread semantics Intra-thread semantics are the standard semantics for single threaded programs, and allow the complete prediction of the behavior of a thread based on the values seen by read actions within the thread. To determine if the actions of thread t in an execution are legal, we simply evaluate the implementation of thread t as would be performed in a single threaded context, as defined in the remainder of the Java Language Specification.

Each time evaluation of thread t generates an inter-thread action, it must match the inter-thread action a of t that comes next in program order. If a is a read, then further evaluation of t uses the value seen by a.
Simply put, intra-thread semantics are what result from the execution of a thread in isolation; when values are read from the heap, they are determined by the memory model.

Synchronization Actions All inter-thread actions other than reads and writes of normal and final variables are synchronization actions.

Synchronization Order In any execution, there is a synchronization order which is a total order over all of the synchronization actions of that execution. For each thread t, the synchronization order of the synchronization actions in t is consistent with the program order of t.

Happens-Before Edges If we have two actions x and y, we use $x \xrightarrow[]{hd} y$ to mean that x happens-before y. If x and y are actions of the same thread and x comes before y in program order, then $x \xrightarrow[]{hd} y$.
Synchronization actions also induce happens-before edges:

• There is a happens-before edge from an unlock action on monitor m to all subsequent lock actions on m (where subsequent is defined according to the synchronization order).
• There is a happens-before edge from a write to a volatile variable v to all subsequent reads of v (where subsequent is defined according to the synchronization order).
• There is a happens-before edge from an action that starts a thread to the first action in the thread it starts.
• There is a happens-before edge between the final action in a thread T1 and an action in another thread T2 that allows T2 to detect that T1 has terminated. T2 may accomplish this by calling T1.isAlive() or doing a join action on T1.

In addition, we have two other rules for generating happens-before edges.

• There is a happens-before edge from the write of the default value (zero, false or null)of each variable to the first action in every thread.
• Happens-before is transitively closed. In other words, if $x \xrightarrow[]{hd} y$ and $y \xrightarrow[]{hd} z$, then $x \xrightarrow{hd} z$.

Execution Trace An execution trace (which we sometimes simply call an execution) E of a program P consists of four parts:

• A set of inter-thread actions, including, for each thread t, the program order among actions in thread t.
• A synchronization order over the synchronization actions in the execution.
• The happens-before relationships in the program, derived from the program order and the synchronization order.
• A causal order, discussed in Section 7.

This tuple is written as ⟨S, so,$\xrightarrow{hd}$, co⟩. An execution trace E is a valid execution trace if and only if

• the actions of each thread obey intra-thread semantics
• and the values seen by the reads in E are valid according to the memory model (as defined in Section 6 – 10).

The use of fields marked final changes the guarantees for write visibility somewhat. Final fields are frequently guaranteed to see their correctly initialized value regardless of happens-before orderings. This is discussed in detail in Section 8.
The wait methods of class Object have lock and unlock actions associated with them; their happens-before relationships are defined by these associated actions. These methods are described further in Section 12.

# Consistency

We first introduce a simple memory model called consistency.
The happens-before relationship defines a partial order over the actions in an execution trace; one action is ordered before another in the partial order if one action happens-before the other. We say that a read r of a variable v is allowed to observe a write w to v if, in the happens-before partial order of the execution trace:

• r is not ordered before w (i.e., it is not the case that $r \xrightarrow{hd} w$), and
• there is no intervening write w$\rq$ to v (i.e., no write w$\rq$ to v such that $w \xrightarrow{hd} w\rq \xrightarrow{hd} r$).

Informally, a read r is allowed to see the result of a write w if there is no happens-before ordering to prevent that read. An execution trace is consistent if all of the reads in the execution trace are allowed.
Because consistent execution traces do not have causal orders, they are represented by a tuple ⟨S, so,$\xrightarrow{hd}$⟩.

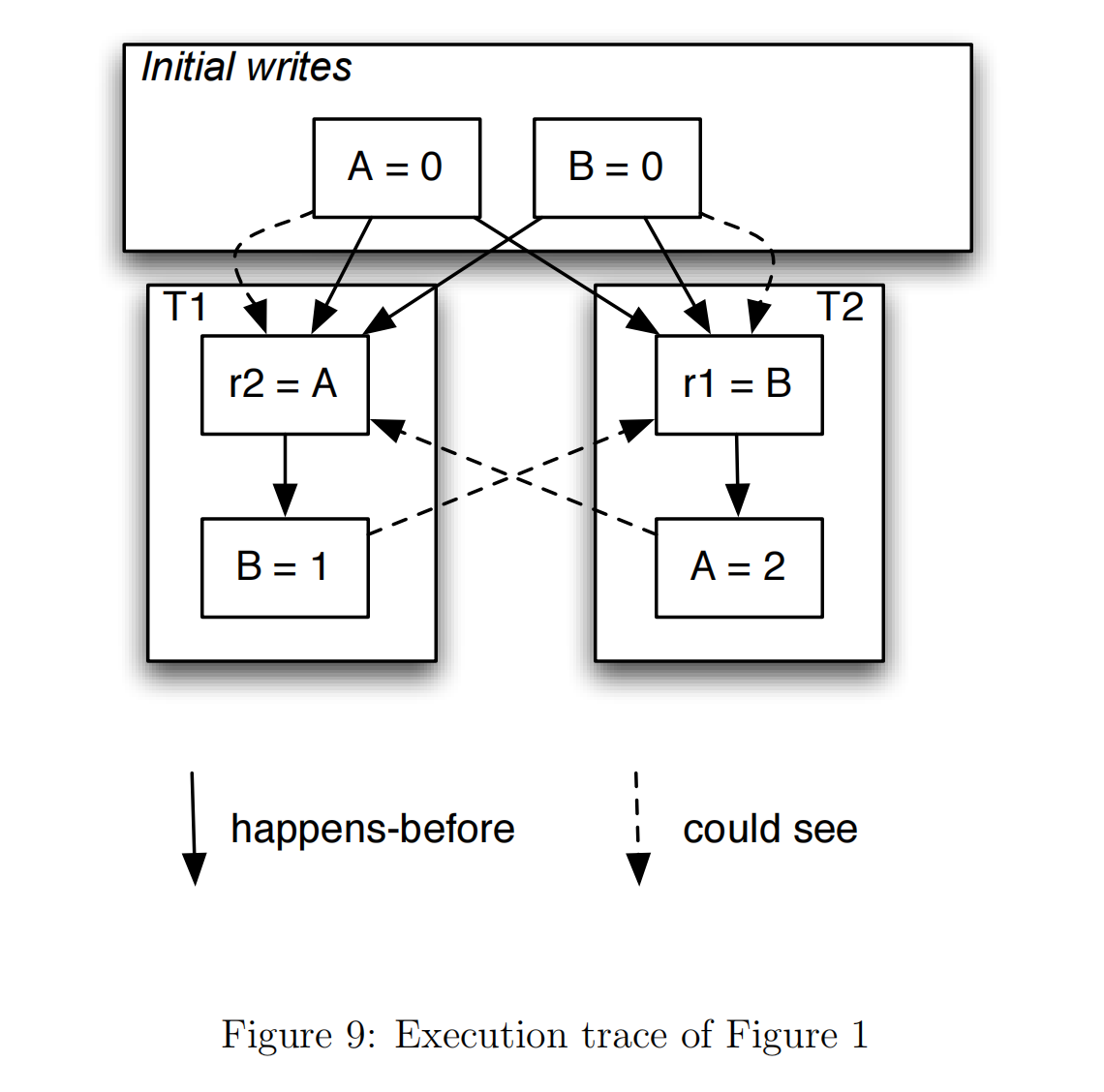
As an example of this simple model, consider Figure 1, and the corresponding graph in Figure 9. The solid lines represent happens-before relationships between the actions. The dotted lines between a write and a read indicate a write that the read is allowed to see.
For example, the read at r2 = A is allowed to see the write at A = 0 or the write A = 2.
An execution is consistent, and valid according to the Consistency memory model, if all reads see writes they are allowed to see. So, for example, an execution that has the result r1 == 1, r2 == 2 would be a valid one.

# Causality

Consistency is a necessary, but not sufficient, set of constraints. In other words, we need the requirements imposed by Consistency, but they allow for unacceptable behaviors.
In particular, one of our key requirements is that correctly synchronized programs may exhibit only sequentially consistent behavior. Consistency alone will violate this requirement.
Consider the code in Figure 10. If this code is executed in a sequentially consistent way, each action will occur in program order, and neither of the writes will occur. Since no writes occur, there can be no data races: the program is correctly synchronized. We therefore only want the program to exhibit sequentially consistent behavior.
Could we get a non-sequentially consistent behavior from this program? Consider what would happen if both r1 and r2 saw the value 1. Can we argue that this relatively nonsensical result is legal under Consistency?
The answer to this is “yes”. The read in Thread 2 is allowed to see the write in Thread 1, because there is no happens-before relationship to prevent it. Similarly, the read in Thread 1 is allowed to see the read in Thread 2: there is no synchronization to prevent that, either. Consistency is therefore inadequate for our purposes.
Even for incorrectly synchronized programs, Consistency is too weak: it can allow situ-ations in which an action causes itself to happen, when it could happen no other way. We say that an execution that contains this behavior contains a causal loop. At the extreme, this might allow a value to appear out of thin air. An example of this is given in Figure 11. If we decide arbitrarily that the writes in each thread will be of the value 42, the behavior r1 == r2 == 42 can be validated as consistent: each read each sees a write in the execution, without any intervening happens-before relation.
To avoid problems such as this, we require that executions respect causality. It turns out that formally defining causality in a multithreaded context is tricky and subtle.

# Causal Orders

For any execution trace, we require the existence of a causal order, which is an ordered list of the reads, writes and synchronization actions in that execution. The causal order can be considered an explanation of how an execution happened. For example, first we can show that x could happen; once we know x will happen, we can show that y can happen; once we know that both x and y will happen, we can show that z can happen.

The causal order does not have to be consistent with the program order or the happens-before order. Any total order over actions in an execution trace is potentially a valid causal order. The causal order could, for example, reflect the order in which the actions might occur after compiler transformations have taken place.
The intuition behind causal orders is that for each prefix of that causal order, the next action in the order is justified by the actions in the prefix. Actions that do not involve potential cycles do not need to be explicitly justified; we only require the justification of prescient actions. An action x in a trace ⟨S, so,$\xrightarrow{hd}$, co⟩ is prescient if and only if either:

• there exists an action y that occurs after x in the causal order such that $y \xrightarrow{hd} x$ or
• x observes a write that occurs after it in the causal order.

All prescient actions must be justified. To justify a prescient action x in trace E, let α be the actions that occur before x in the causal order. We need to show that x will be allowed to occur in all executions with a causal order that starts with α and contains no prescient actions after α. Section 7.4 describes an alternative weak causality model, in which we would only require that there exist some execution in which x would be allowed to occur.
It should be fairly clear that there are no causal orders for which Figure 11 will produce 42: there is no sequence of actions that will guarantee that 42 will be written to x or y.
In addition, the reads in Figure 10 will not be able to see the value 1. The first action in the causal order would have to be a write of 1 or a read of 1. Since neither of those are allowed in any non-prescient execution, they cannot be the first action in a causal order.

Formally defining causality is somewhat involved. To do so, it is necessary to define what it means for one action to be in more than one execution. This definition will be omitted here; the full definition can be found, along with the formal model, in Appendix B.

# When is a race read justified in a causal order?

We need to state more formally what it means for a read r to be justified in occurring in an execution E whose causal order is αrβ. If r is involved in a data race, then execution can non-deterministically choose which of the multiple writes visible to r is seen by r, which makes it difficult to guarantee that r will see a particular value. The read r is justified if in all executions whose causal order consists of α followed by non-prescient actions, there is a corresponding read r$\rq$ that is allowed to observe the same value that r observed.
Intuitively, we are only able to justify a read if it will always be allowed to occur based on the actions we have already justified.

# Prohibited Sets

In order to perform an action presciently, we must be guaranteed that the action will occur.
The JMM allows for many possible behaviors of incorrectly synchronized programs. Com-pilers may perform transformations that prevent some behaviors that are allowed by the JMM. When these behaviors are prohibited by compiler transformations, other actions may be guaranteed that were not guaranteed given the full freedom of the JMM. The semantics need to allow such actions to be performed presciently. In Figure 12, we see an example of such an optimization. The compiler can

• eliminate the redundant read of a, replacing 2 with r2 = r1, then
• determine that the expression r1 == r2 is always true, eliminating the conditional branch 3, and finally
• move the write 4: b = 2 early.

Here, the assignment 4: b = 2 seems to cause itself to happen. Thus, simple compiler optimizations can lead to an apparent cyclic execution trace without a workable causal order.
We must allow these cases, but also prevent cases where, if r1 $\ne$ r2, r3 is assigned a value other than 1.
To validate such an execution we would need a causal order that makes r1 == r2 == r3 == 2 a causally consistent execution of Figure 12. To see this behavior, we need a causal order over valid executions that would justify this behavior in an execution.
How would we go about trying to construct a causal order to validate this behavior? In this case, we are trying to capture a potential behavior of the transformed program: the case where 4 happens first, then all of Thread 2, and finally 1 - 3. This would suggest { 4, 5, 6, 1, 2, 3 } as a potential causal order.
However, we cannot use this causal order assuming only Causality and Consistency. The prefix of 4 (b = 2) is empty, so all of the validated executions for which the empty set is a prefix (i.e., all validated executions) must allow the write 4 to occur. The problem is that 4 is not guaranteed to occur in all non-prescient executions; it only occurs whenever r1 and r2 see the same value. If we were able to exclude all executions in which r1 and r2 see different values, then we could use the causal order { 4, 5, 6, 1, 2, 3 }
In short, compiler transformations can make certain executions (such as the ones in which 1 and 2 do not see the same value) impossible. This prohibition, in turn, can lead to additional executions that seem cyclic.
For the purposes of showing that a prescient action x is justified, a set of behaviors that are not possible on a particular implementation of a JVM may be specified. This, in turn, allows other actions to be guaranteed and performed presciently, allowing for new behaviors.
If we allowed arbitrary executions to be prohibited, we could conceivably, for example, prohibit all executions. We could then vacuously justify any action we liked, because it would occur in every execution. This sort of behavior is nonsensical; we therefore cannot allow arbitrary executions to be prohibited.
Instead, an execution can be prohibited only if it contains a read that could see multiple values, and there is an alternate execution that is not prohibited that contains that read, but sees a different value.
Consider prescient action x in an execution $⟨S, so,\xrightarrow{hd}, \alpha x \beta⟩$ we wish to justify, and the set of executions J of executions whose causal order starts with α. We allow the specification of a set of prohibited executions $P \subset J$, and only require that x be allowed to occur in all executions in $J-P$.
For each prohibited execution $E\rq \in P$, we must identify a read r in $E\rq$, but not in $\alpha$, that is allowed by the happens before constraint to see multiple writes. Assume that in $E\rq$ the read r sees a write w. Then there must exist a different write $w\rq$ that could be seen by r in $E\rq$ and an execution $E\rq\rq \in J-P$ such that

• r and $w\rq$ occur in $E\rq$, and in $E\rq\rq$, the read r sees $w\rq$.
• $E\rq\rq$ includes all of the actions that come before r in the causal order of $E\rq$.

Note that since r represents a choice at which $E\rq$ and $E\rq\rq$ diverge, the remainder of their executions can be substantially different.
Using prohibited executions, we can show that the execution in Figure 12 respects causal-ity. This can be done by prohibiting all executions where h1 and h2 do not return the same value. Execution traces where they do return the same value can be provided as alternate executions.

# Causality Model Summary and a Possible Weakening

Figure 15 summarizes, using the informal notation used in this section, the strong causality model proposed for the Java Memory Model. However, the JSR-133 expert group is debating whether instead to adopt a weaker model (Figure 16) that would make fewer guarantees about the behavior of incorrectly synchronized programs and might allow for more compiler and other optimizations of Java programs. At the moment, we do not have a good handle on whether guarantees necessary for safety and defensive programming might be violated by the weaker model, or whether there are any compiler or architectural optimizations that would be forbidden by the stronger causality model. The expert group solicits feedback on this issue. The weak causality model allows the behavior shown in Figure 14, while this behavior is forbidden by the strong causality model.